ƒ(x) = anxn + an-1xn-1 +... + a2x2 + a1x + a0
The exponents are whole numbers only. The constant term a0=a0x0
Coefficients ai are any real numbers; except an≠0.
Terms can be "missing/absent": when the coefficient ai=0
Already should be simplified and in decreasing exponent order.
Polynomial is simple: each term (monomial) is only multiplication (positive integer power) of variable and by coefficient. A sum of products.
Examples:
ƒ(x)= 4x5-6x3+1
ƒ(x)= -2x4+5x3+4x2-3x
ƒ(x)= x4-x3-x2-x-1
ƒ(x)= 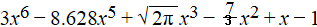
n is the degree of the polynomial. This leading term dominates all the others,
determining the end behavior of the curve.
constant (degree 0) polynomial: a0
linear (degree 1) polynomial: a1x + a0 AKA: mx+b
quadratic (degree 2) polynomial: a2x2 + a1x + a0
AKA: ax2+bx+c
cubic (degree 3) polynomial: a3x3 + a2x2 + a1x + a0
AKA: ax3+bx2+cx+d
quartic: 4th power. ax4+bx3+cx2+dx+e
quintic: 5th power.
degree-6, degree-7, etc.
Domain of every polynomial function is ℝ.
Continuous everywhere (no gaps, holes, jumps, vertical asymptotes in graph).
And smooth (no cusps, corners, kinks).
What you want to know about a polynomial function:
--end behavior, which infinities does it "come from" and "go to".
--x-intercept(s), if any. ≤n of them. (n or n-2 or n-4 or ... or 1 or 0 x-intercept(s)).
And whether the graph crosses the x-axis or touches and rebounds off it.
These are the (real number) roots of the function and solve the equation ƒ(x)=0
(i.e. the real zeroes of the equation).
--y-intercept. is the constant term, a0, or 0 if there is no constant term.
--turning points, if any, where the graph changes from decreasing to increasing,
or vice versa, and is horizontal at that one point, and is
a global or local extremum. ≤n-1 of them.
This is the "wiggle" of the polynomial function's graph.
The wiggle could be symmetric, it could be lopsided,
or, in the case of odd-degree polynomial, it might not have any turning points at all.
Also: where it's positive, where negative. Where increasing, where decreasing. Symmetry (even/odd), if any.
Life of a polynomial function: it comes from one of the infinities, does some wiggling, then goes off
to one of the infinities.
Mathpapa can graph them and do some factoring. WolframAlpha can factor, find roots (x-intercepts) and extrema. Desmos too.
A polynomial function of only one term is called a power function:
f(x)=axn
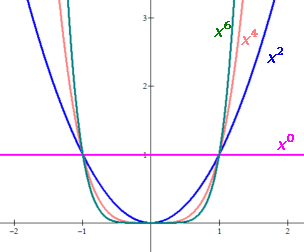
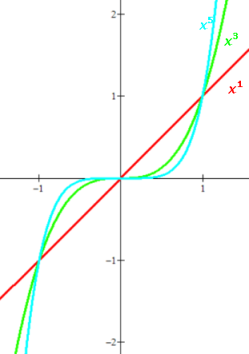
These here all have a=+1
Note the "steepening" and "flattening" as the exponents increase.
Note that the even-degreed power functions are even functions and the odd-degreed
power functions are odd functions, the origin of these words.
Range of polynomial function: end behavior of graph always go to ±∞
Leading term determines the end behavior. because it dominates the function as |x| gets large.
The lesser terms do not affect the end behavior, they only effect the "wiggle".
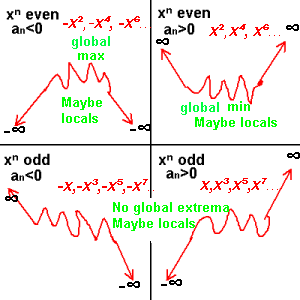
Even degree, e.g. quadratic, quartic, sixth-degree...: "half open".
Either both ends go up, or both go down.
If an<0 then ƒ first increases from -∞ to ymax then decreases to -∞.
i.e. both "ends" point down to -∞.
If an>0 then ƒ first decreases from +∞ to ymin then increases to +∞.
i.e. both "ends" point up to +∞.
Odd degree, e.g. linear, cubic, quintic...: Range is ℝ. One end goes up, the other goes down.
If an<0 then ƒ decreases from +∞ to -∞.
i.e. left "end" points up to +∞, right "end" points down to -∞
If an>0 then ƒ increases from -∞ to +∞.
i.e. left "end" points down to -∞, right "end" points up to +∞
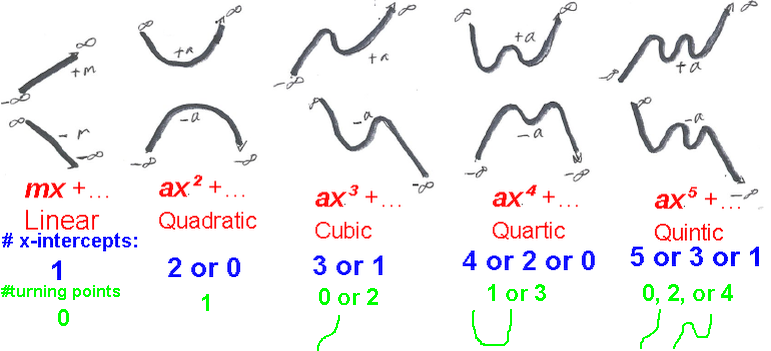
Number of x-intercepts is ≤ degree n.
(Odd degree has at least one: the graph goes from one infinity to the other,
so has to cross the X-axis;
the corresponding polynomial equation has at least one real solution).
More precisely, there are either n or n-2 or n-4 or ... or 1 or 0 x-intercepts
(counting multiplicities).
The x-intercepts are the zeros of the corresponding polynomial equation, i.e.
solve the polynomial=0, what values of x make the polynomial 0.
A polynomial can be factored into linear polynomials (linear binomials)
and irreducible quadratic polynomials (which have a pair of complex conjugate solutions).
In general, factoring is very hard, so use software to do it or approximate it.
The number of turning points is at most degree-1. Calculus is needed to find the (non-zero) turning points.
y-intercept is (0,f(0)) = (0,a0), the constant term.
Changing the constant term raises/lowers the entire graph (without affecting its shape),
possibly changing the number of x-intercepts.
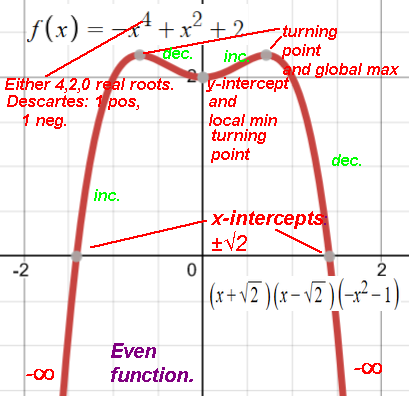
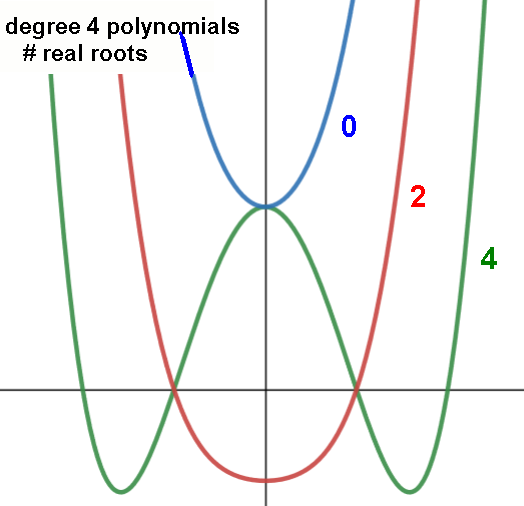
Example: a quartic polynomial ax4+... can have 0, 2, or 4 real roots/x-intercepts
and 1 or 3 turning points. If the coefficient a of the quartic term is positive
both ends of the graph curve are +∞, if it is negative the ends are -∞:
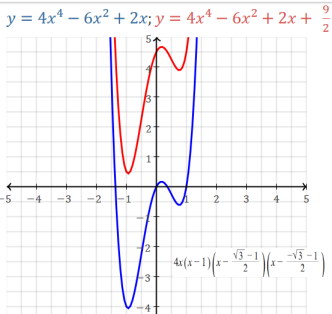
(change the constant term to 1 to see two x-intercepts case.)
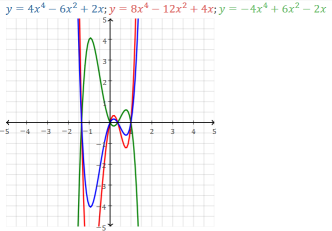
All multiples of a polynomial function have the same x-intercepts
(as all multiples of a polynomial equation have the same solutions.):
Multiplicity, repeating of roots/x-intercepts:
even multiplicity: touch/rebound x-axis
odd multiplicity: cross/cut x-axis
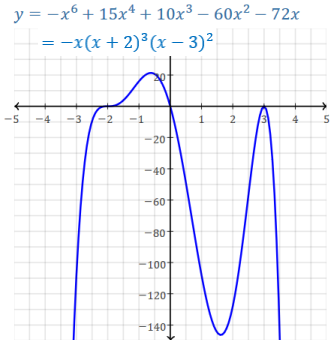
This function has x-intercepts: 0 once (odd multiplicity), 3 twice (even multiplicity),
-2 thrice (odd multiplicity) for a total of 1+2+3= 6 roots.
Sum, difference, product, and composition of two polynomial functions is polynomial.
Quotient of two polynomial functions p(x)/q(x) is a rational function.
Polynomial equation in standard form:
anxn + an-1xn-1 +... + a2x2 + a1x + a0 = 0
A root is c such that ƒ(c)=0. i.e. c is a solution of this equation.
Has n roots/zeroes (some of which might be non-real complex numbers,
which, if the polynomial has only real coefficients, are
complex conjugates (pairs of the form a+bi and a-bi)).
Has up to n real roots/zeroes/x-intercepts:
even-degreed: 0 or 2 or 4 or ... n.
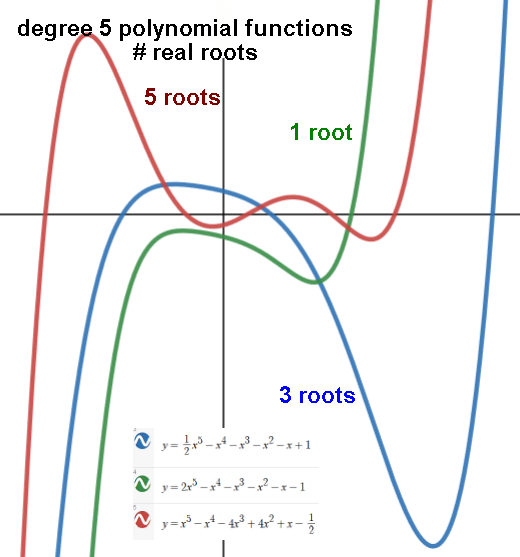
odd-degreed: 1 or 3 or 5 or ... n.
A rational root/zero/x-intercept c is a linear factor (x-c).
Completely factorable iff all roots are rational?
A rational-coefficients polynomial equation is equivalent to an integer-coefficients polynomial equation
(multiply both sides by the LCD). A rational-coefficients polynomial function kP(x) is a multiplicative
factor (LCD k) of an integer-coefficients polynomial function P(x) and has the same zeroes.
Formulas exist for solving linear, quadratic, cubic (Cardano), and quartic (Ferrari/Tartaglia)
polynomial equations,
but no higher (Abel/Galois: impossible to exist).
Linear: to solve 0=mx+b x=-b/m
Quadratic formula: to solve 0=ax2+bx+c
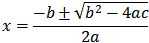
Cubic formula: square roots of negative numbers needed.
To solve 0=ax3+bx2+cx+d
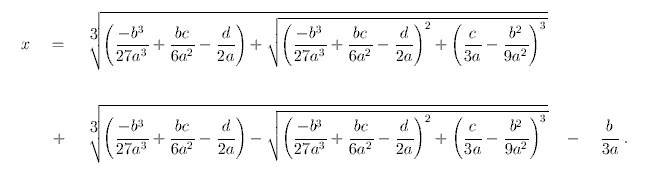
Quartic too complicated...
Factor theorem:
(x-c) is a (linear) factor of P iff c is a zero (f(c)=0), i.e. can divide P by (x-c).
P/(x-c) = Q(uotient) polynomial.
Fundamental theorem of algebra:
Every polynomial function as at least one complex zero.
Every polynomial equation has at least one solution.
A polynomial of degree n has n linear
factors (x-ci) which can be real, complex, repeated.
(Repeated real roots of even multiplicity are the touching-the-x-axis intercepts.)
The set of these linear factors is unique.
A polynomial can be factored into linear factors (x-c), where c is a solution to the
equation and an x-intercept, and irreducible quadratic factors whose roots
are a pair of complex conjugates.
***The number of real zeros/x-intercepts is either n, n-2, n-4, ...down to 0 if n is even,
or 1 if n is odd (every odd-degree polynomial function has at least one x-intercept).
[reserving pairs of complex conjugate roots].
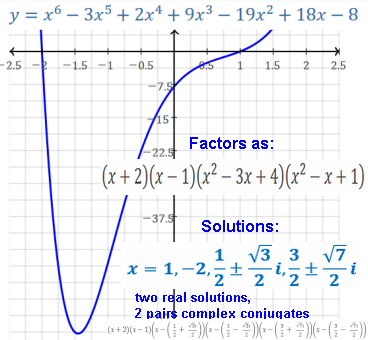
Rational roots theorem:
the only possible rational roots of a polynomial with integer coefficients
are of the form p/q where p is an integer factor
of a0 and q is an integer factor of an.
Example: a polynomial with integer coefficients.
Only the leading coefficient and the constant are needed:
6xn + ... + 4 = 0
p=4, integer factors are ±{1, 2, 4}
q=6, integer factors are ±{1, 2, 3, 6}
All quotients p/q: ±{1,2,4,1/2,1/3,1/6,2/3,4/3}.
Any rational roots of this polynomial are in this set.
If no constant term, 0 is a root (y-intercept is 0, thus passes thru origin)
but no rational roots? or theorem not applicable?
If an is 1, then only integers that are factors of the constant p are possible rational factors.
If an, a0, and the sum of all the coefficients are all odd,
then there are no rational roots.
Not very useful?
Descartes' rule of signs:
To help with finding the number of roots (x-intercepts).
--number of positive real roots is either the number of sign changes in P(x)
or any multiple of 2 fewer (due to complex conjugate pair roots)
--number of real negative roots is either the number of sign changes in P(-x)
or any multiple of 2 fewer (due to complex conjugate pair roots).
Example:
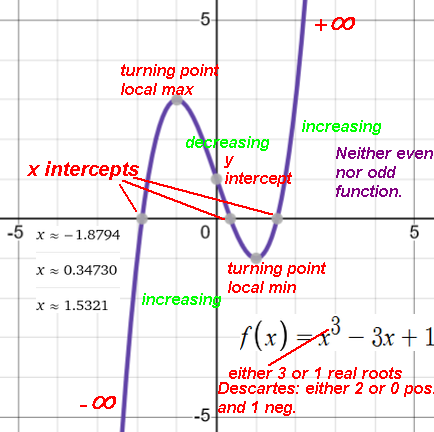
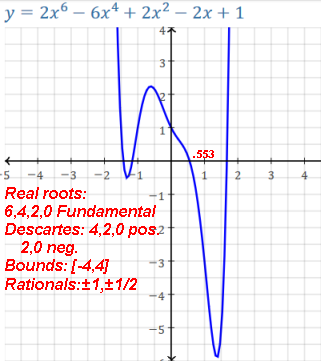
P(x): 3x4-5x3-3x2+x-6=0 has 3 sign changes, so it has either 3 or 1 positive root(s).
P(-x): 3x4+5x3-3x2-x-6=0 has 1 sign change, so it has 1 negative root.
NB. in P(-x) only the xodd terms change sign:
Ex. If P(x)= x5+x4+x3+x2+x+1
then P(-x)= -x5+x4-x3+x2-x+1
Ex. If P(x)= -x5-x4-x3-x2-x-1
then P(-x)= x5-x4+x3-x2+x-1
Tip: MP @x=-x
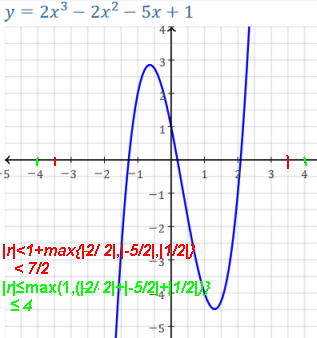
Bounding the roots.
Any real root / x-intercept r of a polynomial function
is bounded by:
|r| ≤ max{1, (|an-1/an| + |an-2/an| +...
+ |a1/an| + |a0/an|)}
or by:
|r| < 1 + max{|an-1/an|, |an-2/an|,...,
|a1/an|, |a0/an|}
A real zero/root/x-intercept lies between any a and b such that f(a) and f(b) have opposite signs,
by the intermediate value theorem.
Can be used by the bisection method to numerically approximate a root.
Summary:
Fundamental theorem says how many roots: A degree-n polynomial has n roots,
which can be real or complex conjugate pairs. NB. count the multiplicities.
The number of real roots is any number from n downto 1 for odd n, 0 for even n,
decreasing by 2.
Ex. a degree-5 polynomial could have 5, 3, or 1 real roots. A degree-6 could
have 6,4,2,0 real roots.
The real roots are the x-intercepts of the function.
Descartes says how many possible positive and negative (real) roots.
The real roots are within the interval around 0 of the smallest of the above bounding values.
Rational roots theorem (if integer coefficients) says possible rational roots.
Factor theorem says can divide P by (x-c), c a root.
Can factor a polynomial into linear binomials and irreducible quadratics.
Each of the former yields a real root, each of the latter a pair of complex conjugate roots.
Polynomial:
Easy to differentiate: each term (aixi)'=iaixi-1
and to integrate: each term ∫aixi=(ai/(i+1))xi+1 +c
Interesting:
x3-2x-1 = (x+1)(x2-x-1) = (x+1) (x-φ)(x+φ-1)
x5-2x3-x2
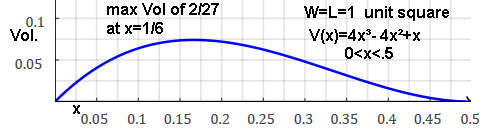
Open-top box made by cutting same-sized squares from four corners of a rectangle and then folded:
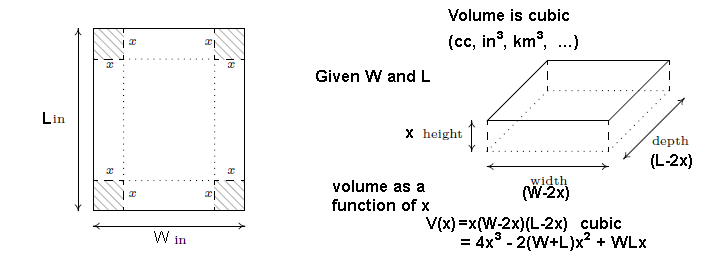
Make a box from the unit square:
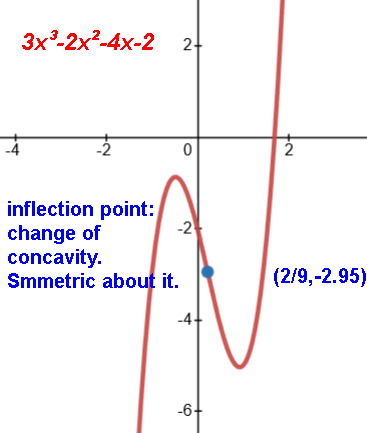
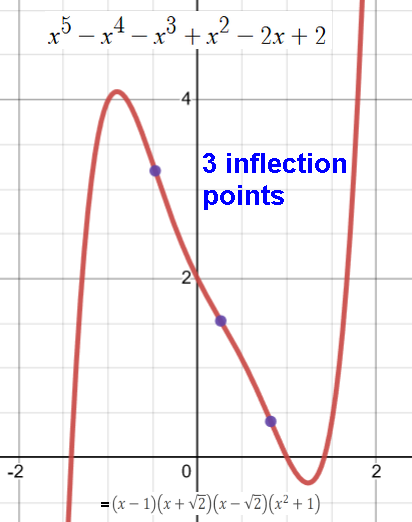
Cubic function has inflection point (-b/3a, f(-b/3a)). symmetric about it.
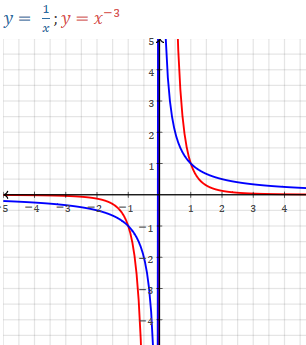
NB. f(x)= x-n are not polynomial (exponents must be positive integers, not negative)
x-n = 1/xn
n even:
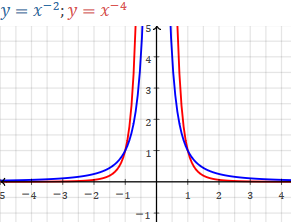
n odd: