Binomial distribution

You try/do something a few (n) times, each time/try/trial having the same chance (p) of succeeding/winning/happening/scoring. What's the chance that you succeed(ed) in some (k) of those trials? 0≤k≤n

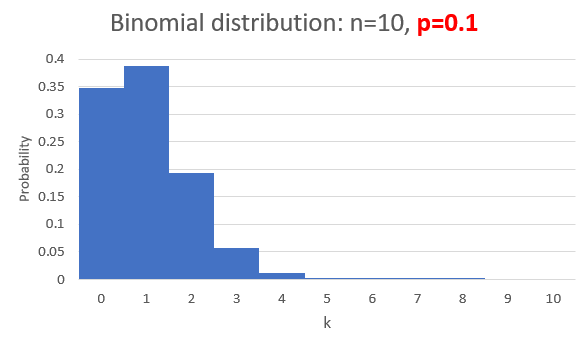
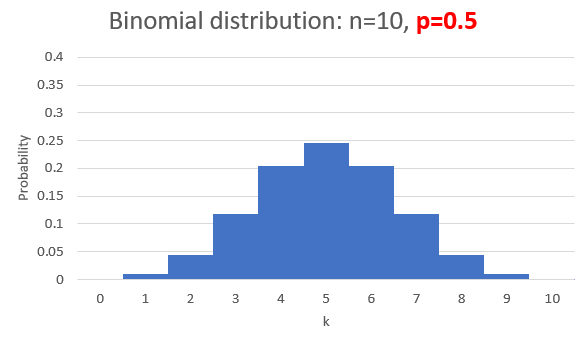
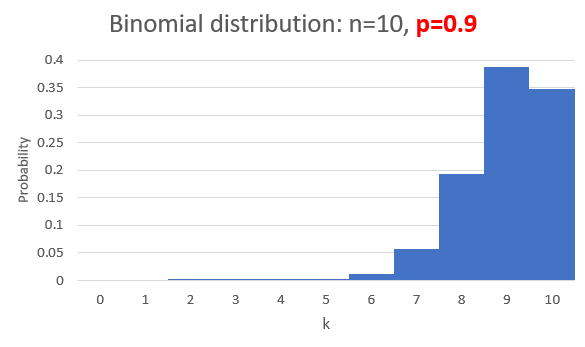
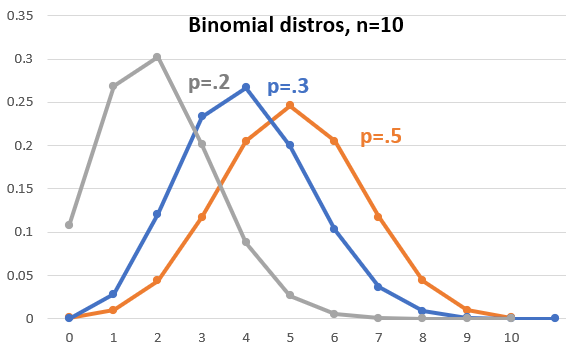
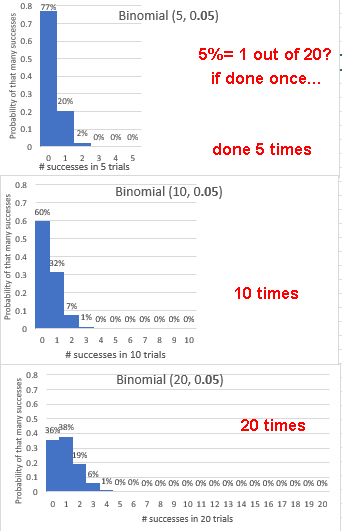
In a sample of size n from a population that proportion p have a certain feature what's the chance that 0, 1, 2, ..., n of the sample have the feature?

The number of successes in a sequence of n independent experiments, each asking a yes-no question, and each with its own boolean-valued outcome: success/yes/true/one (with probability p) or failure/no/false/zero (with probability q = 1 - p).
NB. "success" could mean getting a disease, dying, losing money, etc.

The sample space S = {0,1,2,3,...,n}   i.e. the number of successes, k.
P(k) the probability that in the n trials there will be k successes:
    P(k)=     k=0,1,...,n
The nCk is the number of positionings of where the k successes can be.
Alternate notation: let Χ be a random variable, P(Χ=x) =
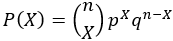      X=0,1,...,n

Ex.: A fair coin (p=0.5) is tossed. In n=10 tosses what is the probability of achieving k=0, k=1, 2, 3,..., k=10 heads?
Ex.: Today there is a 30% chance of rain. On n=5 similar days, what are the chances that it didn't rain (k=0), it rained on one day (k=1), it rained on two days (k=2), ..., it rained on all five days (k=n=5)? It rained on at least one day?
Ex.: If you make 80% of your shots/throws/kicks/whatevers, what are the chances that in a game of n=6 attempts you make none of them (k=0), all of them (k=n=6), and each number k between 0 and 6?
Ex.: A biased coin comes up heads with probability p=0.3 when tossed. In n=5 tosses what is the probability of achieving k=0, k=1,..., k=5 heads?
Ex.: From a large population having a certain feature with probabilty p draw a sample of size n. [color blindness 8%] What are the probabilities that k=0, k=1, k=2, ..., k=n items have the feature?
Ex.: A process has a 60% chance of success. What are the probabilities that in k=0, k=1,...,k=n applications of the process success occurs?

When k=n, i.e. all n trials are successful, P(n)=pn.
When k=0, i.e. all n trials are failures, P(0)=qn.
The probability of at least one success in the n trials is the sum of the P(1),P(2),...P(n) which is 1-P(0) which equals 1-qn.

Number of independent trials/experiments (n):
Probability of success per trial [0..1] (p):

Mean= np:
Standard deviation= √(npq): (NB. when p=0.5 the SD is √n/2)

  k       nCk       pk       qn-k        P(k)      ΣP(k)=CDF=P(≤k)   P(≥k)

Show a particular k:   
exactly k: P(k)=    at most k: CDF is ∑P(k)=    at least k: P(≥k)=

Probability histogram:

Bernoulli distribution is a binomial distribution with n=1 trial. Done once, two possible outcomes of chances p and 1-p.
E[X]=p
V[X]=p(1-p)
σ=√(p(1-p))
p σ
.1 .3
.5 .5
.6 .4899
.9 .3

A binomial random variable is the sum of n independent identical Bernoulli random variables. Each of the n trials is Bernoulli, i.e has only two possible outcomes. The random variable is the number of successes.

As n gets larger, a binomial distribution tends to Normal.
Faster if p is closer to .5:

Binomial probability distribution can be approximated by the Poisson probability distribution with λ=np when np<5 or nq<5.

Excel: Binom.Dist(k, n, p, TRUE/FALSE) FALSE for PMF, TRUE for CDF.

True/False test: n questions. chance of passing (≥50%)=
Multiple choice test (either 4 or 5 choices): n questions. chance of passing (≥50%)=

Twin rate 2%, random sample of 1000. μ= , σ= 

X:      0     1     2    3
P(X): .064  .288  .432 .216
Binomial distro?  n= , p=