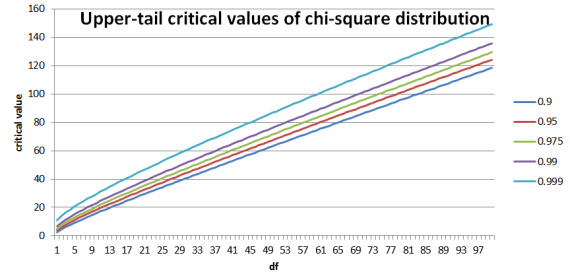
Chi-squared Χ2 test of goodness-of-fit (GOF)

See whether a frequency distribution fits a specific pattern.
Applied to categorical data to evaluate how likely it is that differences between the actual observed data and its expected/theoretical values arose by chance.
It tests a null hypothesis that the frequency distribution of certain events observed in a sample is consistent with a particular theoretical distribution. The events must be mutually exclusive and have total probability 1.

Observed values Oi:
Expected values Ei : (AKA Theoretical values) All should be ≥5.

Select a desired level of confidence (significance level, 1-α level) for the result of the test:

0.90 0.95 0.975 0.99 0.999

p: Theoretical distribution's number of parameters; reduction in df. (usually 1, but 3 for Normal, 2 for Poisson)

ΣOi=N=
degrees of freedom df= the number of categories reduced by the number of parameters of the fitted distribution, i.e. n-p degrees of freedom, where n is the number of categories, p the number of parameters.
   Resembles a normalized sum of squared deviations between observed and theoretical frequencies. Asymptotically approaches a Χ2 distribution.

Χ2 statistic=       critical value=      p_value:
If Χ2 test statistic > critical value, then reject the null hypothesis (H0 that there is no difference between the distributions, i.e. it is a good fit), and the alternative hypothesis (HA that there is a difference between the distributions, i.e. that it is not a good fit) is supported, at the selected level of confidence. Informally, the observed data does not fit the expected distribution.
If Χ2 test statistic < critical value, then, informally, the observed data does fit the expected distribution.
Χ2 test statistic is a measure of the discrepancy between Observed and Expected frequencies. The worse the fit, the larger is Χ2.

The non-uniform Ei examples can be visualized in Visualize Two Dependent Samples
Roughly, if it's all/mostly vertical lines, it fits.

Excel: Line chart w/marker
category Oi Ei 

video. die 30 rolls:
#1s #2s #3s #4s #5s #6s
 3   3   4   8   7   5
Expected uniform distro: 1/6*30
 5   5   5   5   5   5

book: 45 die rolls:
13   6  12   9   3  2
Expected uniform distro: 1/6*45
7.5 7.5 7.5 7.5 7.5 7.5 

book: loaded die 45 rolls
13    6   12   9   3  2
22.5 4.5 4.5 4.5 4.5 4.5 

last digit of self-reported weights  n=2784
1175 44 169 111 112 731 96 110 171 65
every E= 1/10*2784= 278.4  Expected uniform distro

Benford's law E
.301 .176 .125 .097 .079 .067 .058 .051 .046

Leading digits packet interarrival time
69 40 42 26 25 16 16 17 20    =271
271*Ei:
81.571 47.696 33.875 26.287 21.409 18.157 15.718 13.821 12.466

76 62 29 33 19 27 28 21 22
95.417 55.792 39.625 30.749 25.043 21.239 18.386 16.167 14.582


V-1 hits. #of the 576 London regions with 0,1,2,3,4 hits of 535 hits
229 211 93 35 8
227.5 211.4 97.9 30.5 8.7     expected Poisson u=.929

Kentucky Derby
19 14 11 15 16 7 9 12 5 11   =119
every E=119/10= 11.9

Old Faithful.  classwidth 10. Drop outlier 125   n=49
2 0 3 9 23 10 2
hmm, won't work on tails? <5   "can be combined with another class"
0.0029 0.0259 0.1165 0.2690 0.3191 0.1947 0.0610

Skittles colors   233 "of 4 bags"
Oi:   43 50 44 44 52
Ei:   44.6 44.6 44.6 44.6 44.6

The day-of-birth data in Nominal Data
n=400, each day equally likely, so Ei =400/7= 57.14 

Mendel's 556 pea seeds
% smooth-yellow smooth-green wrinkled-yellow wrinkled-green
Oi:  0.5666 0.1942 0.1816 0.0556
Ei:  0.5625 0.1875 0.1875 0.0625
*556:
315.0 108.0 101.0 30.9
312.7 104.2 104.2 34.8
Fisher said : BS, too good to be true

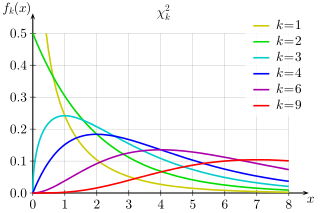
PDFs of chi-squared functions for first few values of k:

Area under each curve is 1.

Sum of k squared random selections from the standard normal distribution.
Expected value of Χ2k = k
Variance of Χ2k = 2k

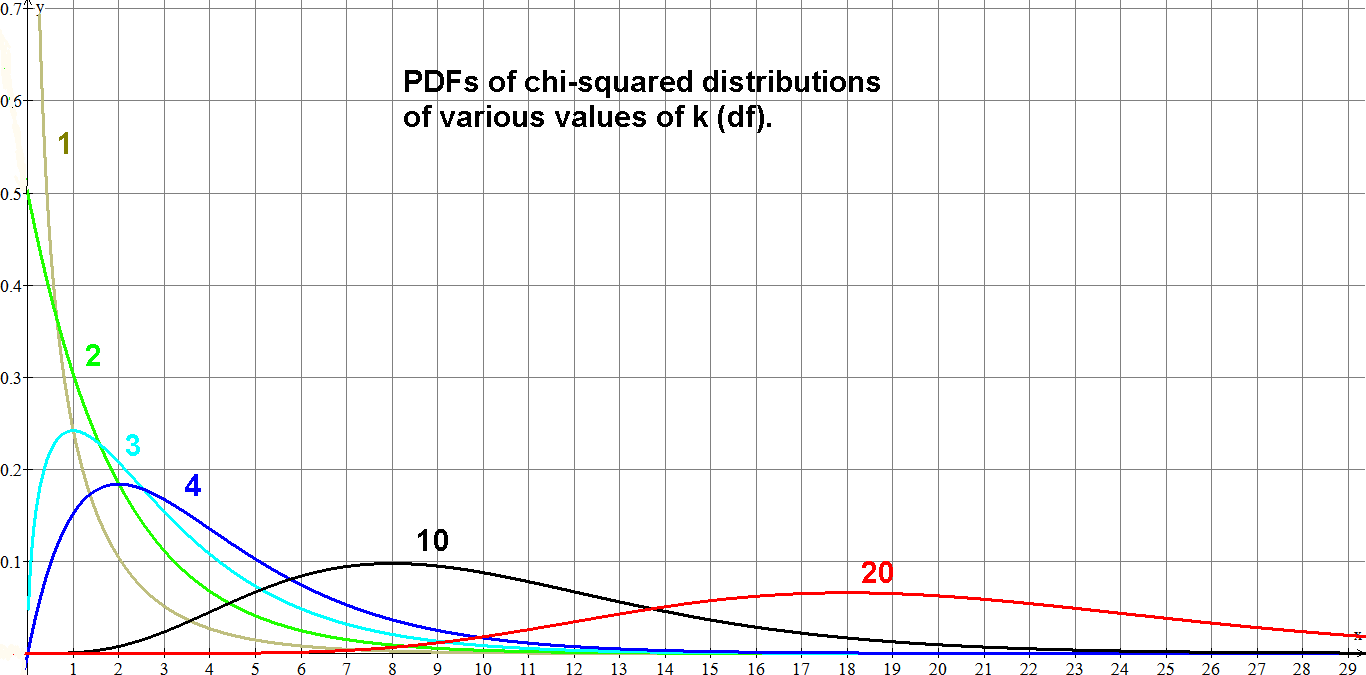
PDFs of chi-squared functions for various values of k:

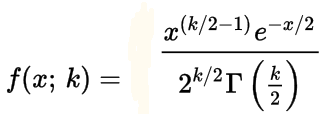Γ gamma function

k Γ(k/2) =/≈
1 Γ(1/2) 1.7724
2 Γ(1) 1
3 Γ(3/2) .8862
4 Γ(2)=1! 1
5 Γ(5/2) 1.3293
6 Γ(3)=2! 2
7 Γ(7/2) 3.3233
8 Γ(4)=3! 6
9 Γ(9/2)
10 Γ(5)=4! 24
20 Γ(10)9! 362880 

Mathpapa k= 1, 2, 3
y=\frac{x^{\left(\frac{1}{2}-1\right)}e^{-\frac{x}{2}}}{2^{\frac{1}{2}}\cdot 1.7724}\ \ ;\ \ \ \ y=\frac{x^{\left(\frac{2}{2}-1\right)}e^{-\frac{x}{2}}}{2^{\frac{2}{2}}}\ ;y=\frac{x^{\left(\frac{3}{2}-1\right)}e^{-\frac{x}{2}}}{2^{\frac{3}{2}}\cdot .8862}